Optik illüzyonlar ve bulmacalar örtüşen hisleri paylaşıyor. Zihinsel kandırmaca, ‘aha’ anları, şaşı hayal kırıklığı. Nöral Korelasyon Derneği’nin bir organizasyona sahip olduğunu biliyor muydunuz? yıllık yarışma Yılın En İyi İllüzyonu için? Bu yılın kazananı, Harry Potter’ın Platform 9 ¾’ünün görünüşte geçirgen bir tuğla duvarla tamamlanan bir LEGO modelini yarattı:
Bu düzgün ayna gösterisi son finalistler arasında da öne çıkıyor. Bu haftanın bulmacalarının yanıltıcı bir doğası var. Önümüzdeki Pazartesi çözüm yazısında ne demek istediğimi açıklayacağım.
Geçen haftaki bulmacayı kaçırdınız mı? Buna bir bak Buradave çözümünü bugünkü makalenin alt kısmında bulabilirsiniz. Geçen haftanın sorununu henüz çözmediyseniz çok ileriyi okumamaya dikkat edin!
Bulmaca #19: Zihinsel Yanılsamalar
1. 100 karınca bir ölçüm çubuğunun üzerine aynı anda rastgele konumlardan düşüyor. Her karınca, dakikada bir metre hızla, çubuğun sol veya sağ ucuna doğru rastgele yürümeye başlar. Karıncalar seçtikleri yola devam ederler, ancak iki karınca çarpıştığında ikisi de hemen yön değiştirir ve aynı hızla ters yönde yürümeye devam ederler. Tüm karıncaların çubuğun ucundan uzaklaşması için gereken en uzun süre nedir?
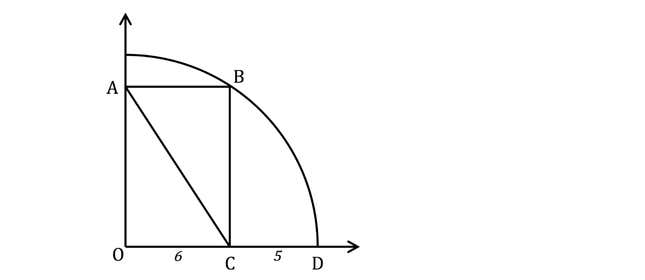
2. Merkezi O olan bir dairenin çeyreğinin içine bir dikdörtgen yazılmıştır. Dikdörtgenin AC köşegeninin uzunluğunu bulun.
Gelecek hafta çözümlerle ve yeni bir bulmacayla geri döneceğim. Burada ele almam gereken harika bir bulmaca biliyor musun? Bana Twitter’dan mesaj at @JackPMurtagh veya bana [email protected] adresinden e-posta gönderin
Bulmaca #18’in Çözümü: Uzun Salon
Geçen haftaki finans iş görüşmesi sorusu paran için sana bir şans mı vereceğim?
Tam kareler (1, 4, 9, 16, 25, 36, 49, 64, 81 ve 100) sonunda açılacak olan tek kapıdır. Şuna bağır: bilmece88 sebebini çıkardığım için.
Nedenini görmek için a’nın tanımını hatırlayın. bölen matematik dersindeki ilk günlerinden beri. Bir sayının bölenleri, o sayıyı kalansız olarak bölen sayılardır. Örneğin, 12’nin bölenleri şunlardır: 1, 2, 3, 4, 6 ve 12. Her kapının, bölenlerine karşılık gelen turlar sırasında değiştirildiğine dikkat edin (örneğin, 8. kişi içeri girdiğinde, 8, 16 numaralı kapılar). , 24, 32 vb. değiştirilir, ancak 12, 8’e bölünemediğinden kapı 12’ye dokunulmaz. 12 numaralı kapı kapalı olarak başladığından ve çift sayıda değiştirildiğinden (altı böleni vardır), kapalı konumda sona erecektir. Böylece soru şu oluyor: Hangi sayıların tek sayıda böleni vardır?
Bölenler çiftler halinde gelme eğilimindedir. 1, 12 ile çarpıldığında 12 olur, dolayısıyla 1 ve 12’nin her ikisi de bölendir. 2, 6 ile çarpıldığında 12 olur, yani her ikisi de bölendir ve böyle devam eder. Yani bölenleri çift olmayan tek sayılar, bir sayının çarpılmasıyla elde edilebilen sayılardır. kendisi ile. Örneğin, 16’nın bölenleri 1, 2, 4, 8 ve 16’dır. 1 çifti 16 ile, 2 çifti 8 ile kapalıdır ve 4’ün kendisi ile çarpıldığından 16 olduğu için 4’ün ortağı yoktur. mükemmel kareler tam olarak tek sayıda böleni olan sayılardır ve bunlar sonunda açılan kapılardır.
Bu bulmacayı seviyorum çünkü mükemmel kareler birdenbire ortaya çıkıyor gibi görünüyor. Kurulumda bunların kokusu yok. Pek çok kişinin kare sayılara aşinalığı vardır, ancak bunların tek sayıda böleni olan tek sayılar olarak nitelendirilmesinin birçok okuyucu için yeni olacağından şüpheleniyorum.
