Hayatta kalan 45 sezon gibi muazzam bir sezon üretti ve daha fazlası da geliştirme aşamasında. 1. sezonla ilgili söylentileri hatırlıyorsanız ancak 45 yıl geçtiğine inanamıyorsanız, öyle değil. Doyumsuz hayran kitlelerini beslemek için sezonun çoğunu yılda iki sezon çıkardılar. Her sezon, çok başarılı bir realite şovu, tropik bir adada bir milyon dolarlık ödül için yarışan kestane renginde çatışan kişiliklerden oluşan çekici bir kadroyu gösteriyor. Yarışmacılar, hayatta kalma ekipmanı kazanmak veya gösteriden çekilmeye karşı bağışıklık kazanmak için fiziksel, dayanıklılık ve zihinsel zorluklara maruz kalıyor. Ada hızla entrikalar ve arkadan bıçaklamalarla dolu bir düdüklü tencereye dönüşüyor, bu da izleyicilerin hoşuna gidiyor.
Bu haftanın bulmacası, dizinin Tayland’da geçen 5. sezon galasında kullandığı gerçek bir zihinsel mücadeleden kaynaklanıyor. Bir strateji oyununda iki takım rekabet eder, ancak keşfedeceğiniz gibi, bir takım her zaman doğru hamlelerle galibiyeti zorlayabilir. Kazazedeler gerçek zamanlı olarak en uygun stratejiyi bulmakta başarısız oldular, bunun yerine bir takım için çok geç olana kadar hatalar yaptılar. Zaman baskısı altında bu anlaşılabilir bir durum, ancak bazı taraftarlar yenilmez bir stratejinin varlığının oyunu adaletsiz hale getirdiğinden yakınıyor.
Bunu bunaltıcı bir kumsalda, yüzünüze televizyon kameraları varken çözebileceğinizi düşünüyorsanız bana bildirin. İyi şanslar; kabileniz size güveniyor.
Geçen haftaki bulmacayı kaçırdınız mı? Buna bir bak Buradave çözümünü bugünkü makalenin alt kısmında bulabilirsiniz. Geçen haftanın sorununu henüz çözmediyseniz çok ileriyi okumamaya dikkat edin!
Bulmaca #30: Hayatta kalan Bayraklar
Jeff Probst yere 21 bayrak dikti. A Kabilesi ve B Kabilesi dönüşümlü olarak bir, iki veya üç bayrağı aynı anda kaldıracaktır (sıfıra izin verilmez). Son bayrağı kaldıran kabile kazanır. Eğer A Kabilesi ilk giderse, Hangi takım galibiyeti zorlayabilir ve kazanma stratejisi nedir?
Gelecek Pazartesi çözüm ve yeni bir bulmacayla geri döneceğim. Burada yer alması gerektiğini düşündüğünüz harika bir bulmaca biliyor musunuz? Bana Twitter’dan mesaj at @JackPMurtagh veya bana e-posta gönderin [email protected]
Bulmaca #29’un Çözümü: Sportif Bir Şans
Zaferle çıktın mı son haftalarda rekabetçi bulmacalar?
Super Bowl’u kaçırdım. Tek bildiğim, iki takımın yetenek açısından mükemmel bir şekilde eşleştiği (inanmamayı bir kenara bırakın) ve skorun Olumsuz devre arasında berabere kaldı. İlk yarıyı geride bırakan takımın geri dönüp maçı kazanma şansını bilmek istiyorum. Yalnızca bu bilgi göz önüne alındığında, şansı neye koymalıyım?
Mükemmel eşleşme derken, takımların farklı skorlara ulaşma olasılıklarının aynı olduğunu ve dahası bu olasılıkların oyun durumuna (yani hangi yarıda olduklarına veya kimin önde olduğuna) bağlı olarak değişmediğini kastediyorum. Super Bowl maçlarının berabere bitemeyeceğini unutmayın: İkinci yarıdan sonra skorlar eşitse uzatmalara gidilir.
İlk yarıyı geride bırakan takımın geri dönüp maçı kazanma şansı %25’tir. Oyunun her yarısını ayrı ayrı düşünün. Tüm beraberlikleri göz ardı edeceğiz çünkü bize ilk yarıda maçın berabere bitmediği söylendi ve oyunun berabere bitmesine izin verilmediğini biliyoruz. A ve B takımlarını çağıralım ve diğer yarıyı göz ardı ederek her yarıda kimin “kazandığını” not edelim. Dört olasılık vardır: AA, AB, BA, BB (örneğin BA, B’nin ilk yarıda A’dan daha fazla puan aldığı, ancak A’nın ikinci yarıda B’den daha fazla puan aldığı anlamına gelir).
Elbette sadece her yarıyı kimin kazandığı değil, aynı zamanda ne kadar kazandığı da önemli. BA’da B, ilk yarıda 40 sayı farkla kazanabilirken ikinci yarıyı sadece 2 puan kaybetmiş olabilir ve bu nedenle yine de tüm oyunu kazanır. Tüm olasılıkları bir tabloya yerleştirelim:
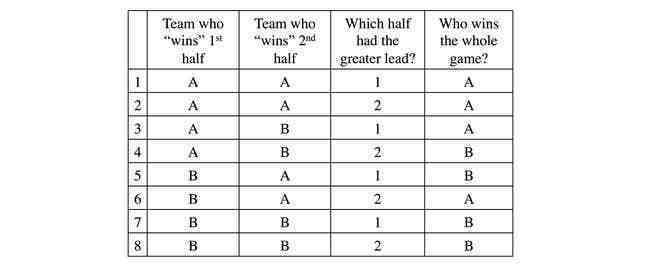
Önemli bir anlayış, takımlar eşit şekilde eşleştiğinden, sekiz olasılığın hepsinin eşit olasılıkla gerçekleşmesidir. Her iki takımın da her iki yarıda da daha fazla sayı atma şansı 50/50’dir. Ve ilk yarının, ikinci yarıya göre daha büyük veya daha küçük bir farka sahip olma ihtimali eşit. Sekiz sıradan yalnızca ikisi (%25), devre arasında geride kalan takımın geri döndüğü oyunları belirtir: 4. sıra ve 6. sıra. Örneğin, 5. sıra, A’nın devre arasında geride kaldığı ve ikinci yarıda B’den daha fazla gol atmasına rağmen olduğu anlamına gelir A’nın açığını kapatmaya yetmedi.
Dr. Emilio Lizardo %25’lik doğru cevabı tahmin etti çünkü futbol yayınları sıklıkla bu rakamı aktarıyordu. Bir bağlantı paylaştı Bu makale Bu, neredeyse 40 yıllık NFL maçlarını inceliyor ve devre arasında lider olan takımın yüzde 73 ila yüzde 82 oranında kazandığını gösteriyor. Bir NBA maçlarının analizi %74,8 oranında ilk yarıda önde olan takımın maçı kazanmaya devam ettiğini buldu. Yani bu basitleştirilmiş model bir şeylerin peşinde olabilir!
Şimdi geçen haftanın bonus bulmacasına geçelim.
Birkaç takım basit bir eşleştirme turnuvasına katılır (yani her takım diğer takımlarla bir kez oynar). Turnuvadaki diğer tüm takımlar ya onlara yenilirse ya da kendilerine kaybeden birine yenilirse, o takımı süper kazanan olarak adlandırın. Her turnuvanın en az bir süper kazananı olduğunu iddia edin.
Şuna bağır: Eugenius Bonus bulmacanın mükemmel ve kısa bir çözümü için.
En çok maç kazanan takıma bakın. Eğer bağ varsa bunlardan herhangi birini seçin. Onlara Keçiler adını verelim. The Goats’ı seçtik çünkü hiçbir takım onlardan daha fazla oyun kazanamadı. Keçilerin süper kazananlar olması gerektiğini iddia ediyorum. Diyelim ki onlar değildi süper kazananlar. Bu varsayım bir çelişkiye yol açacak ve The Goats’ın aslında süper kazananlar olduğu sonucuna varmamızı sağlayacak.
Eğer süper kazananlar değilse, o zaman The Goats’ı yenen, onlara The Underdogs diyelim, bir takım olmalı Ve The Goats’ın yendiği herkesi yendim. Ancak bu, Underdogs’un The Goats’tan daha fazla oyun kazandığı anlamına gelir! Çünkü Underdogs, Goats’ın yendiği her takımı yendi artı Keçiler kendileri. Hiç kimse The Goats’tan daha fazla oyun kazanamadı, dolayısıyla bu bir çelişki ve varsayımımız yanlış olmalı: The Goats aslında süper kazananlardı.
